性能优化 Critical Dependency Chains
在体系结构中,只有RAW(read after write) data hazard叫做true dependency,意味着后续读指令必须等待前面的指令输出结果。而WAW,WAR等情况都可以用寄存器重命名的方法解决。
鉴于这种特性,在软件编写中,应当注意dependency chains带来的性能影响。
1. 分析关键路径
现在假设我们CPU访问一次L1 data cache延迟4个周期,不考虑读指令的延迟,再假设分支预测百分百正确且无延迟,其他指令都需要执行一个周期。再假设这个CPU有无限的function unit,一次可以issue任意多指令,只要这些指令的输入数据已经就绪。
1.1 数组求和
loop:
rCurInt = load64(rCurPtr); // Load
rSum = rSum + rCurInt; // Sum
rCurPtr = rCurPtr + 8; // Advance
if rCurPtr != rEndPtr goto loop; // Done?
上面的伪汇编代码就是执行一段数组求和,由于 Load 指令需要4个周期,且 Advance 指令和 Load 指令之间没有数据依赖,CPU可以在第一个周期同时开始执行 Load 指令和 Advance 指令。一个周期后,Load 指令还没有出结果,但是新的rCurPtr已经计算完成。再因为我们假设了分支预测一定准确且无延迟,则在第2个周期可以 Load 新rCurPtr的数据,并同时计算下一个rCurPtr的值,整个过程如下
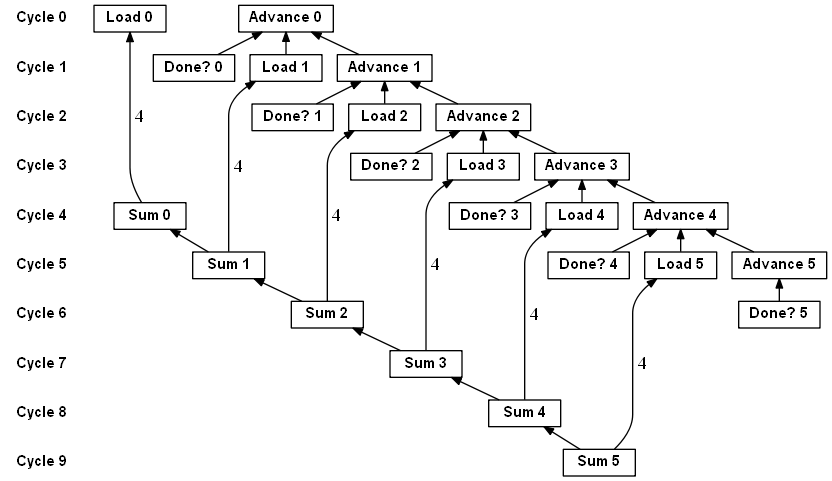
虽然每个 Load 需要4个周期来完成,但因为CPU可以乱序执行,最终的效果还是每个周期可以计算一次求和。
重看上面的代码,很可能下意识认为性能瓶颈在于 Load 操作,因为它有最大的延迟。但是,现代CPU完全可以安排其他指令来乱序执行,只要保证和 Load 没有依赖关系就好。事实上,处于 critical path 的是 Advance 指令,因为 loop 循环的下一轮指令中,全都直接或间接依赖 Advance 的结果。也就是说,只有 Advance 出结果了,我们才能并行执行下一轮迭代中的指令。在数组求和中看不出 Advance 的重要性是因为其延迟为1,确实影响不大,下面把数组求和换成链表求和。
1.2 链表求和
loop:
rCurInt = load64(rCurPtr); // LoadInt
rSum = rSum + rCurInt; // Sum
rCurPtr = load64(rCurPtr + 8); // LoadNext
if rCurPtr != rEndPtr goto loop; // Done?
和数组求和区别只是在于 LoadNext 需要访问L1 cache,延迟4个周期而不是 Advance 只需要一个周期,链表求和的运行结果如下
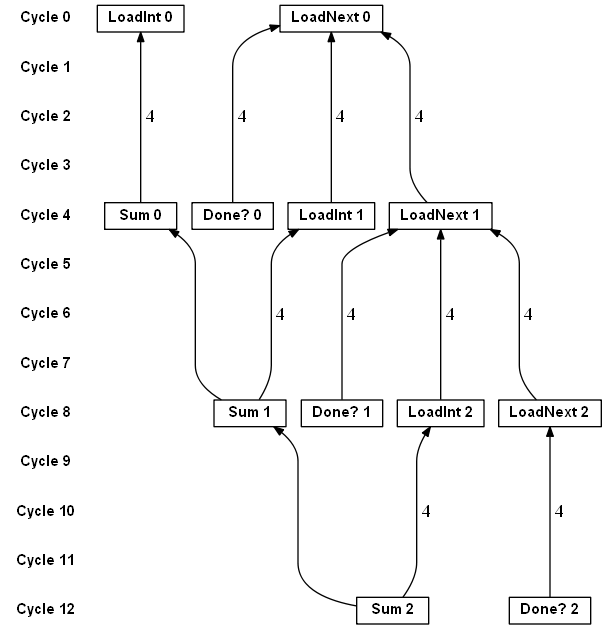
现在,每4个周期才能做一次求和,性能大幅下降,这就是说为什么 Advance 是在关键路径上。想象一下,在数组求和的场景,Load 延迟增加4倍而不是 Advance 增加4倍,那么最后的效果仍然是每个周期做一次加法,只不过需要花更多时间来占满流水线,影响有限。
1.3 粒子移动
再举一个更实际的例子,假设我们模拟粒子随机移动
// The number of motion simulation steps.
constexpr uint32_t STEPS = 10000;
// The number of paticles to simulate.
constexpr uint32_t PARTICLES = 1000;
struct Particle {
float x;
float y;
float velocity;
};
// Initialize the particles with random coordinates and velocities.
std::vector<Particle> initParticles();
// Medium-quality random number generator.
// https://www.javamex.com/tutorials/random_numbers/xorshift.shtml
struct XorShift32 {
uint32_t val;
XorShift32 (uint32_t seed) : val(seed) {}
public:
uint32_t gen() {
val ^= (val << 13);
val ^= (val >> 17);
val ^= (val << 5);
return val;
}
};
constexpr double PI_D = 3.141592653589793238463;
constexpr float PI_F = 3.14159265358979f;
// Approximate sine and cosine functions
// https://stackoverflow.com/questions/18662261/fastest-implementation-of-sine-cosine-and-square-root-in-c-doesnt-need-to-b
static float sine(float x) {
const float B = 4 / PI_F;
const float C = -4/( PI_F * PI_F);
return B * x + C * x * std::abs(x);
}
static float cosine(float x) {
return sine(x + (PI_F / 2));
}
// A constant to convert from degrees to radians.
// It maps the random number from [0;UINT32_MAX) to [0;2*pi).
// We do calculations in double precision then convert to float.
constexpr float DEGREE_TO_RADIAN = (2 * PI_D) / UINT32_MAX;
// Simulate the motion of the particles.
// For every particle, we generate a random angle and move the particle
// in the corresponding direction.
template <class RNG>
void randomParticleMotion(std::vector<Particle> &particles, uint32_t seed) {
RNG rng(seed);
for (int i = 0; i < STEPS; i++)
for (auto &p : particles) {
uint32_t angle = rng.gen();
float angle_rad = angle * DEGREE_TO_RADIAN;
p.x += cosine(angle_rad) * p.velocity;
p.y += sine(angle_rad) * p.velocity;
}
}
核心思想很简单,在每一步为每一个粒子生成一个随机数,根据这个随机数做很多浮点数计算去改变粒子的位置。运行一次上面的randomParticleMotion() 在我的电脑上花费大概18ms。
分析上面的代码,每个粒子的移动完全是独立的,有依赖的是每个循环中 XorShift32::gen() 方法,如果将 gen 方法改为
struct XorShift32 {
uint32_t val;
XorShift32 (uint32_t seed) : val(seed) {}
public:
uint32_t gen() {
uint32_t ans = val++;
ans ^= (ans << 13);
ans ^= (ans >> 17);
ans ^= (ans << 5);
return ans;
}
};
总体运算量不变,但是减少了 gen 方法调用的依赖,在无其他任何修改的情况下,运行一次randomParticleMotion() 只需要10ms,节省快一半的时间。当然,我们这样修改破坏了 XorShift32 的正确实现,这里只是为了说明代码依赖对性能的影响可能很大。
2. 消除依赖
2.1 Loop Unrolling
循环展开是常见的优化手段,有时候编译器都会自动帮我们循环展开。
假如我们将最初的数组求和展开成每个迭代累加2次,代码如下
loop:
rCurInt = load64(rCurPtr); // LoadEven
rSum = rSum + rCurInt; // SumEven
rCurInt = load64(rCurPtr + 8); // LoadOdd
rSum = rSum + rCurInt; // SumOdd
rCurPtr = rCurPtr + 16; // Advance
if rCurPtr != rEndPtr goto loop; // Done?
性能会提高吗?理论分析肯定会,因为loop overhead减少了。所谓loop overhead就是循环中 Advance 和 Done? 的部分,它们不做实际工作,现在loop overhead需要执行的指令数只有原来的一半。
核心的累加部分性能会提升吗?理论上并不会,因为 SumEven 和 SumOdd之间有数据依赖,无法并行执行。最快也是一个周期做一次累加,和不展开本质是一样的。
为了进一步减少这种数据依赖,一种有效且简单的方式是让 SumEven 和 SumOdd 累加到不同的变量上,如下
loop:
rCurInt = load64(rCurPtr); // LoadEven
rSumEven = rSumEven + rCurInt; // SumEven
rCurInt = load64(rCurPtr + 8); // LoadOdd
rSumOdd = rSumOdd + rCurInt; // SumOdd
rCurPtr = rCurPtr + 16; // Advance
if rCurPtr != rEndPtr goto loop; // Done?
rSum = rSumEven + rSumOdd; // FinalSum
这样在一个周期可以做两次累加操作。
(个人觉得原作对这里unrolling的分析比什么塞满流水线的泛泛解释要透彻的多,本质是减少了数据依赖)
参考