OneMore14

The Part-Time Parliament (Paxos)

•

1. The Problem

Paxos岛屿的议会功能就是通过提案，但是议员们在议会中可能随时退出。

1.2 Requirements

每个议员有一个账本，账本内容书写后不可修改。账本记录通过了哪些提案，每个提案包含一个提案编号和提案内容。要求所有议员的账本上，提案内容不能冲突(consistency of ledgers)，如果一个议员的账本上第6324号提案内容是”减税”，那么其他议员账本上的第6324号提案内容也一定要是”减税”。

如果在通过某个提案后所有议员离场，换一批全新议员进场，那么新议员会完全不知道有已经通过的提案，此时可能会通过和之前提案有冲突的新提案。

要保证整个系统liveness，需要要求议会中某个大多数议员群体在一段足够时间内不离开议会，那么所有提案都能通过并记录在所有议员的账本上。

2. The Single-Decree Synod

在本章，讨论的是一次只决定一个提案的算法。第三章再讨论多个提案的算法。

2.1 Mathematical Results

Synod’s decree通过一系列带有序号的ballot(投票)来选择。一次投票会关于一个提案投票，每个议员决定投还是不投。和一个ballot相关的议员称为quorum，一个ballot succeed 有且只有所有quorum中的议员都投票给这个提案。

\(B_{dec}\) A decree (the one being voted on).

\(B_{qrm}\) A nonempty set of priests (the ballot’s quorum).

\(B_{vot}\) A set of priests (the ones who cast votes for the decree).

\(B_{bal}\) A ballot number.

A ballot B was said to be successful iff \(B_{qrm} \subseteq b_{vot}\)。投票序号是依次递增的，但不代表是按顺序投票的，编号大的ballot可能先决议。

Synod协议有3个限制，如果限制满足，则可以证明其一致性和liveness。

\(B1(\beta)\) Each ballot in \(\beta\) has a unique ballot number

\(B2(\beta)\) The quorums of any two ballots in \(\beta\) have at least one priest in common.

\(B3(\beta)\) For every ballot \(B\) in \(\beta\), if any priest in \(B’\)s quorum voted in an earlier ballot in \(B\), then the decree of \(B\) equals the decree of the latest of those earlier ballots.

image-20240320102207634

在编号为14的投票中，这三个quorum只有 三角形 在之前投过票(即使在本轮它没有投票)，所以2和14的decree值要一样。

在编号为27的投票中，F和三角形都投过票，但是最后一轮是5，所以要5和27的decree一样。

定义一个\(vote v\) 由三部分组成

  • \(v_{pst}\) 投票人
  • \(v_{bal}\) 投票编号
  • \(v_{dec}\) 提案内容

再定义 \(MaxVote(b, p, B)\) 表示\(prist \ p\)在ballot集合 \(B\) 中的所有投票(vote)中，满足 \(v_{bal} < b\) 的最大投票。

上面的三个条件就可以形式化为

image-20240416140049794

目前为止都是容易理解的，现在每次投票的quorum也并没有要求人数占大多数，也没有要求所有quorum都必须投票。这些是为了满足上面3个条件而构造出来的具体方法。

接下来证明上面3个条件可以保证一致性。

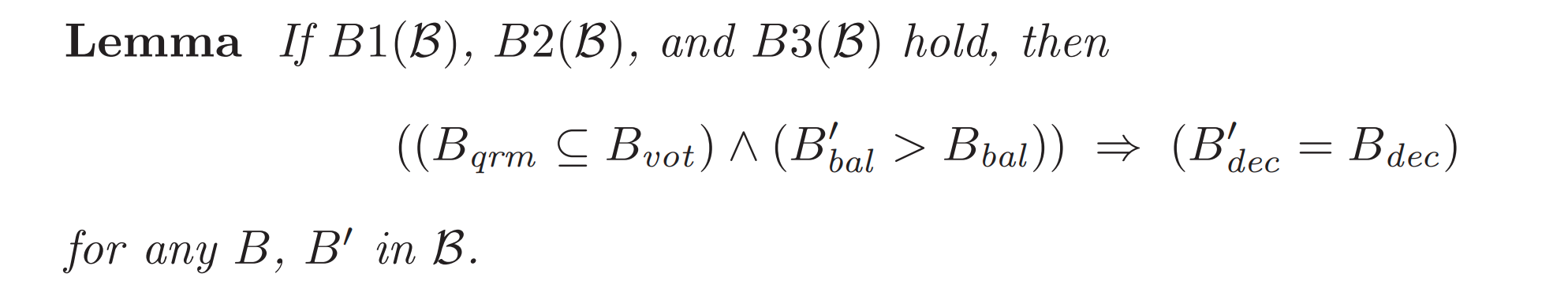
image-20240320144854071

首先引入引理，证明方法见原文(反证法)，其实不用反证法也可以，直接数学归纳法。引理含义是，只要有一轮投票成功了(所有quorum都投了票)，那么之后的所有提案内容一定和这一轮提案相同。

可以得到

Theorem 1

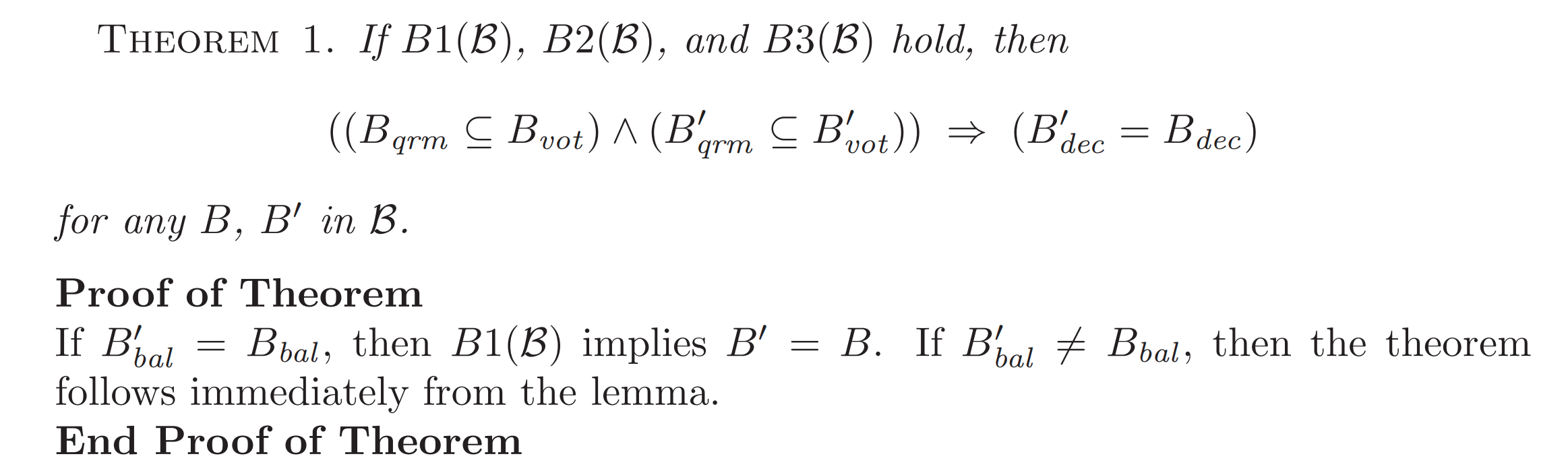
image-20240320155736584

Theorem1的含义是，当投票成功一次后，之后所有成功的投票中，提案内容都一样。

然后有Theorem 2

image-20240320160445686

Theorem 2的意义在于，如果在议会的议员数量足够多(这样每轮投票的quorum不为空)，在保证3个条件的前提下，总能构造出一轮可以成功的投票，且继续满足3个条件。

2.2 The Preliminary Protocol

接下来规定如何发起投票，议员如何决定是否投票，这些规则都要继续满足3个条件。

每个ballot是每个priest提出的，由priest设置ballot的编号，内容和quorum。

为了保证 \(B1\) ，需要每个priest设置ballot的唯一编号，一种解决方法是由priest记录自己发起过的ballot，为了避免两个priest提出相同的id，可以将(id, priest name)组合起来作为ballot 编号。(并不要求全局最大，因为每个priest都可以发起投票)

为了保证\(B2\)，可以priest设置quorum为任意的大多数quorum。

为了保证\(B3\)，需要保证和\(MaxVote(b, Q, B)_{dec}\)一样 (除非其为空)，所以第一步是查询这个值：

  1. Priest \(p\) chooses a new ballot number \(b\) and sends a \(NextBallot(b)\) messag \(e\) to some set of priests.
  2. A priest \(q\) responds to the receipt of a \(NextBallot(b)\) message by sending a \(LastVote(b, v)\) message to \(p\), where \(v\) is the vote with the largest ballot number less than \(b\) that \(q\) has cast, or his null vote \(null_q\) if \(q\) did not vote in any ballot numbered less than \(b\).

所以priest需要记住它之前投过的票。

  1. After receivinga \(LastVote(b, v)\) message from every priest in some majority set \(Q\), priest \(p\) initiates a new ballot with number \(b\), quorum \(Q\), and decree \(d\), where \(d\) is chosen to satisfy \(B3\). He then records the ballot in the back of his ledger and sends a \(BeginBallot(b, d)\) message to every priest in \(Q\).
  2. Upon receipt of the \(BeginBallot(b, d)\) message, priest \(q\) decides whether or not to cast his vote in ballot number \(b\). (He may not cast the vote if doing so would violate a promise implied by a \(LastVote(b' , v' )\) message he has sent for some other ballot.) If \(q\) decides to vote for ballot number \(b\), then he sends a \(Voted(b, q)\) message to \(p\) and records the vote in the back of his ledger.
  3. If \(p\) has received a \(Voted(b, q)\) message from every priest \(q\) in \(Q\) (the quorum for ballot number \(b\)), then he writes \(d\) (the decree of that ballot) in his ledger and sends a \(Success(d)\) message to every priest.
  4. Upon receivinga \(Success(d)\) message, a priest enters decree \(d\) in his ledger.

1-6的每一步都可能消息传递失败或者议员忽略这些消息不做任何行动，但这些都不影响consistency。且因为只有在一次“成功投票”时才会写提案到账本，因此Theorem 1的consistency也是能保证的。

评论:

投票成功与否只和priest是否发送Voted有关，只要发了，无论是否被接收，都会对第2步产生影响。

可以体会一下，每个priest发起的投票编号不同，保证了条件1。每次选择quorum需要保证是大多数，这样保证了条件2。第二步LastVote的保证和第三步选择提案的方式保证了条件3.

为什么要全部quorum投票才写提案到账本？ 假设一共有 n 个议员属于quorum，一共有n - 1个都投了票，而一个议员A没有投票，此时将提案写到账本。在下一轮投票时，恰好A议员是唯一一个同属于两次投票quorum的成员，那么议员A的LastVote就不是上一轮投票中已写入账本的提案，可能会违反一致性要求。

2.3 The Basic Protocol

Basic Protocol只保证consistency，还没有保证liveness。

在2.2的协议中，一个priest必须记录1. the number of every ballot he has initiated 2. every vote he has cast 3. ) every LastVote message he has sent。数据量比较大，下面将其改进成basic protocol，每个priest只需要维护以下数据

  • \(lastTried[p]\) The number of the last ballot that \(p\) tried to initiate, or \(−∞\) if there was none
  • \(prevVote[p]\) The vote cast by \(p\) in the highest-numbered ballot in which he voted, or \(−∞\) if he never voted.
  • \(nextBal[p]\) The largest value of \(b\) for which \(p\) has sent a \(LastVote(b, v)\) message, or \(−∞\) if he has never sent such a message.

basic protocol在2.2节的协议中做一些更严格的限制，不会影响算法的正确性，但是会简化实现。

image-20240321131938677

basic Protocol和2.2 协议一样，每一步都可以不做，因此不保证progress。

2.4 The Complete Synod Protocol

之前的协议全部没有保证progress，因为没有要求priest一定要采取什么动作。

即使我们要求每个priest立即执行(2)到(6)，也要首先保证priest执行第一步，也就是发起提案。但是也不能发起太多提案，如果一直不断发提案，则后面的提案会阻止之前的提案投票，同样没有progress(比如每次投票编号都比之前的大，那basic Protocol的第4步就无法进行)。

首先设置两个值，假设p到q之间的消息传递最多4分钟，p收到事件需要响应最多7分钟(如果有几个消息同时到达，也要保证7分钟)。那么priest预期收到响应的最长等待时间是固定的(从发出消息到接收消息，不应该超过4 + 4 + 7 = 15分钟)，如果没有收到响应，要么是因为对方priest已经下线，要么是因为对方priest收到很多消息需要处理。因此最好是只有一个priest发起提案(至于情况一，priest随机下线是无法避免的)。

考虑p是唯一一个发起投票的人，他被要求在只有在以下两种情况才能发起投票

  1. he had not executed step 3 or step 5 within the previous 22 minutes.(因为 7 + 4 + 7 + 4)
  2. he learned that another priest had initiated a higher-numbered ballot.

那么此时如果议会将 p 和某个大多数议员群体关起来不让走，那么在99分钟内必然有提案通过，且被记录在账本上。99分钟是因为等待发起第一次投票22分钟，然后发起投票结果发现有更高的投票编号，又过去22分钟，重新发起投票且收到足够的LastVote又花22分钟，再计算出提案并收到所有vote又花22分钟，最后发出Success信号需要11分钟(不需要接收对success的确认)。

为了保证只有一个priest发起投票，我们又需要选一个唯一的president。但如果有多个president，只会影响progress，并不影响一致性。选president的方法需要满足以下条件:

If no one entered or left the Chamber, then after \(T\) minutes exactly one priest in the Chamber would consider himself to be the president.

如果上述要求满足，那么在 T + 99的时间内，如果大多数priest都在场且没有人上下线，则能保证最后有一个提案通过。

如果我们以priest名字作为顺序，选择名字最大的作为president。为了满足选举要求，要求每个priest给其他priest发自己的名字，在T-11的时间内。没有收到比自己名字大的priest，就认为自己是president。

3. The Multi-Decree Parliament

之前只是通过一个法案的算法，现在需要通过一系列法案。

3.1 The Protocol

通过多个法案的核心思想是，逻辑上，为每一个法案运行一个Synod Protocol实例，不过实际上都是同一套机器。且为了效率，可以共用一个leader，并且步骤1和步骤2可以同时为所有实例服务，因为在步骤3的时候才真正决定提案的内容。

multi paxos允许Synod Protocol实例间有间隔，比如第100个实例已经通过法案了，但第99个实例还没有。

总的来说，multi paxos描述的篇幅比较少，不是很清晰。

3.2 Properties of the Protocol

3.3 Further Developments

Picking a President

如何选主，有争议，没有统一方法。