Linearizability: A Correctness Condition for Concurrent Objects
评价: Linearizability用时间将不同的process联系起来,是比SC更严格的一致性模型,也更符合现实生活。此外,linearizability具有组合性。
1. INTRODUCTION
1.1 Overview
Linearizability is a local property: a system is linearizable if each individual object is linearizable.
Linearizability is also a nonblocking property: processes invoking totally-defined operations are never forced to wait.
1.2 Motivation
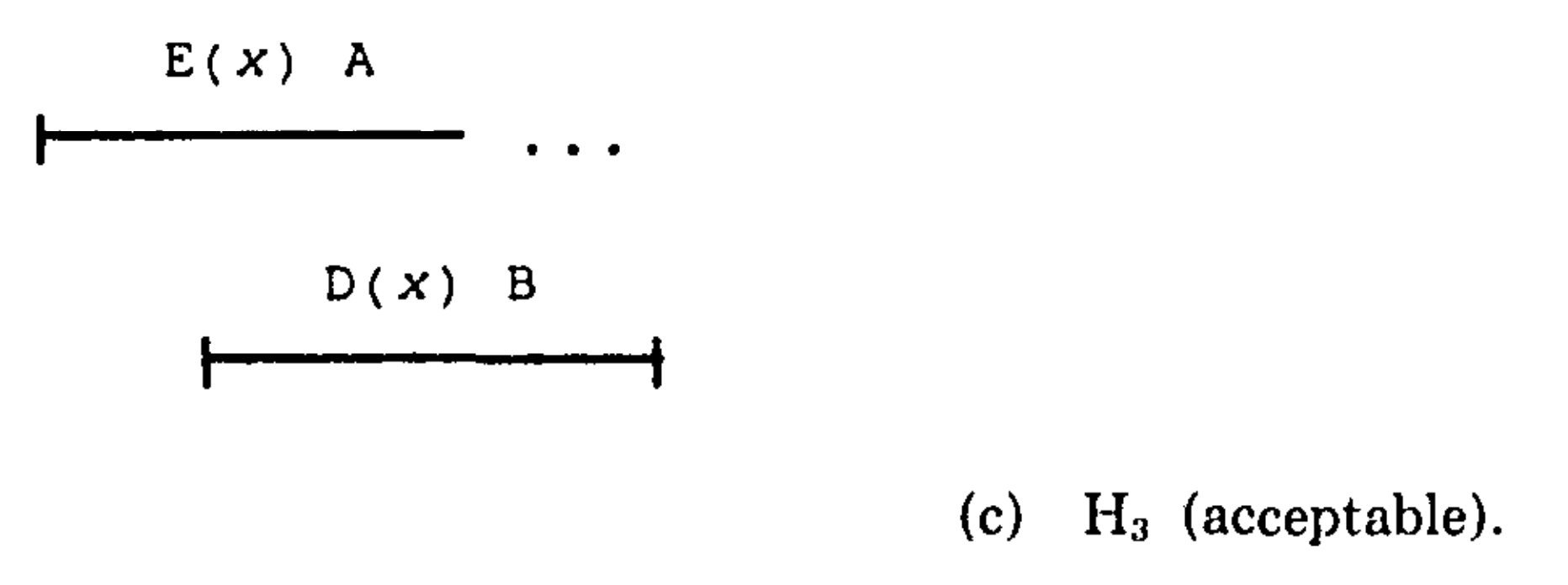
直觉上,即使线程A的入队还没有return,也允许B dequeue成功。
2. SYSTEM MODEL AND DEFINITION OF LINEARIZABILITY
2.1 Histories
历史由一系列操作事件组成,分为invocation和response两种事件,每个事件有对应的进程号(名),变量号(名)。
If \(H\) is a history, complete(\(H\)) is the maximal subsequence of \(H\) consisting only of invocations and matching responses.
A history \(H\) is sequential if:
- The first event of \(H\) is an invocation.
- Each invocation, except possibly the last, is immediately followed by a matching response. Each response is immediately followed by a matching invocation.
process subhistory, \(H \vert P\) 是 \(H\) 中所有属于进程 \(P\) 的事件.
object subhistory \(H \vert x\) 是 \(H\) 中所有属于变量 \(x\) 的事件.
两个历史 \(H\) 和 \(H'\) 是 equivalent ,如果对所有进程\(P\), 有 \(H \vert P = H' \vert P\)
A history \(H\) is well-formed if each process subhistory \(H \vert P\) of \(H\) is sequential. 本文中所有的历史 \(H\) 都认为是well-formed的。(很自然,因为线程本身就是顺序执行的)
A set \(S\) of histories is prefix-closed if, whenever \(H\) is in \(S\), every prefix of \(H\) is also in \(S\).
A single-object history is one in which all events are associated with the same object.
A sequential specification for an object is a prefix-closed set of single-object sequential histories for that object.
A sequential history \(H\) is legal if each object subhistory \(H \vert x\) belongs to the sequential specification for \(x\).
An operation, \(e\), in a history is a pair of consisting of an invocation, \(inv(e)\), and the next matching response, \(res(e)\).
An operation \(e_0\) lies within another operation \(e_1\) in \(H\) if \(inv(e_1)\) precedes \(inv(e_0)\) and \(res(e_0)\) precedes \(res(e_1)\).
An operation is total if, like Enq, it is defined for every object value, otherwise it is partial, like Deq which is left undefined for the empty queue.
2.2 Definition of Linearizability
A history \(H\) induces an irreflexive partial order \(<_H\) on operations:
\(e_0 <_H e_1\) if res(\(e0\)) precedes inv(\(e1\)) in \(H\)
Operations unrelated by \(<_H\) are said to be concurrent.
if \(H\) is sequential, \(<_H\) is a total order.
A history \(H\) is linearizable if it can be extended (by appending zero or more response events) to some history \(H'\) such that:
L1: complete(\(H'\)) is equivalent to some legal sequential history \(S\), and
L2: \(<_H \subseteq <_S\)
将\(H\)扩展成\(H'\) 是为了考虑已经take effect但还没有response的调用, complete(\(H'\)) 是为了考虑还没有take effect的调用。
We call \(S\) a linearization of \(H\). Nondeterminism is inherent in the notion of linearizability, 对每个\(H\),可能有多个不同的\(H'\)存在,对每个\(H'\),也可能有多个满足条件的是\(S\).
2.3 Queue Examples Revisited
对于上面的\(H_3\) ,就可以添加一个E(x) A 的response事件,得到\(H_3'\)。
3. PROPERTIES OF LINEARIZABILITY
证明linearizability的 local 和 nonblocking 性质
3.1 Locality
A property \(P\) of a concurrent system is said to be local if the system as a whole satisfies \(P\) whenever each individual object satisfies \(P\).
Linearizability is a local property.
THEOREM 1. \(H\) is linearizable if and only if, for each object \(x\), \(H \vert x\) is linearizable.
证明, “only if”的部分是显然的。对每个\(x\),选择一个\(H \vert x\)的linearization. Let \(R_X\) be the set of responses appended to \(H \vert x\) to construct that linearization, and let \(<_x\) be the corresponding linearization order. Let \(H'\) be the history constructed by appending to \(H\) each response in \(R_x\). 然后要在complete(\(H'\)) 上构建一个偏序 \(<\),且
(1)对所有\(x\),\(<_x \subseteq <\) ,
(2) \(<_H \subseteq <\) 。
Let \(S\) be the sequential history constructed by ordering the operations of complete(\(H'\))in any total order that extends \(<\). 条件(1)暗示 \(S\) 是legal的,因此L1条件满足,条件(2)暗示满足L2。
我们让\(<\) 是 \(<_H\) 和 \(<_x\)的并集,那么条件(1)(2)是明显满足的,只是要证明\(<\)是partial order。采用反证法,如果其不是partial order,那么一定会存在环 \(e_1 < e_2 < ... < e_n < e_1\). 我们取适当的事件,使这个环的长度最小。
由于每个object \(x\) 的 \(<_x\) 是total order,因此,所有的\(e\) 不可能来自同一个\(x\)。设\(e_1\) 和 \(e_2\) 来自两个不同的object,且\(e1\) 属于 \(x\) .
- 我们先证明,\(e_2, e_3,..., e_n\) 全部都不属于\(x\)。\(e_2\)是显然的,我们构造时就让其不属于\(x\)了。采用反证法,假设存在, 令\(e_i\) 是 \(e_3, e_4,...,e_n\)中第一个属于\(x\)的。 那么 \(e_{i-1}\) 和 \(e_i\) 一定不满足 \(<_x\),而是满足 \(<_H\),即\(e_{i-1}\)的函数返回值在 \(e_i\) 的函数调用前。 此时,\(e_2\)的函数调用一定在\(e_{i-1}\)的函数返回之前,否则就有\(e_{i-1} <_H e_2\) ,这样会构造出一个更小的环,\(e_2, e_3,...,e_{i-1}\),与事实矛盾。根据构造规则,有 \(e_1 <_H e_2\),\(e_1\) 函数返回在\(e_2\)函数调用前,而刚刚已经证明,\(e_2\)函数调用一定在\(e_{i-1}\)函数返回前,且\(e_{i-1}\)函数返回在\(e_i\)函数调用前。于是有 \(e_1\)函数返回在\(e_i\)函数调用前,即\(e_1 <_H e_i\),但这样又组成一条更短的环\(e_1, e_i,...,e_n\),与事实矛盾。因此 \(e_i\) 不存在。
- 由于\(e_n\)不属于\(x\),那么只可能有\(e_n <_H e_1\), 又因为\(e_1 <_H e_2\),所以有\(e_n <_H e_2\),又能构造出更短的环\(e_2,e_3,...,e_n\),与假设矛盾。
因此,\(<\) 一定是partial order。
由此,我们只需要考虑single-object histories. Locality使我们可以采用模块化的方式构造系统。
3.2 Blocking versus Nonblocking
Linearizability is a nonblocking property: a pending invocation defined operation is never required to wait for another pending complete.
THEOREM 2. Let \(inv\) be an invocation of a total operation. If \(<x\ inv\ P>\) is a pending invocation in a linearizable history \(H\), then there exists a response \(<x\ res\ P>\) such that \(H \cdot (x \ res\ P)\) is linearizable.
没看懂证明的方式,且这里只是理论上说明没有blocking,在实际实现上可能会有。
3.3 Comparison to Other Correctness Conditions
Sequential consistency是比linearizability更弱的,因为不保留历史原来的顺序
Enq(x) A
Ok() A
Enq(y) B
Ok() B
Deq() B
Ok(y) B
上面满足SC,但不满足linearizability
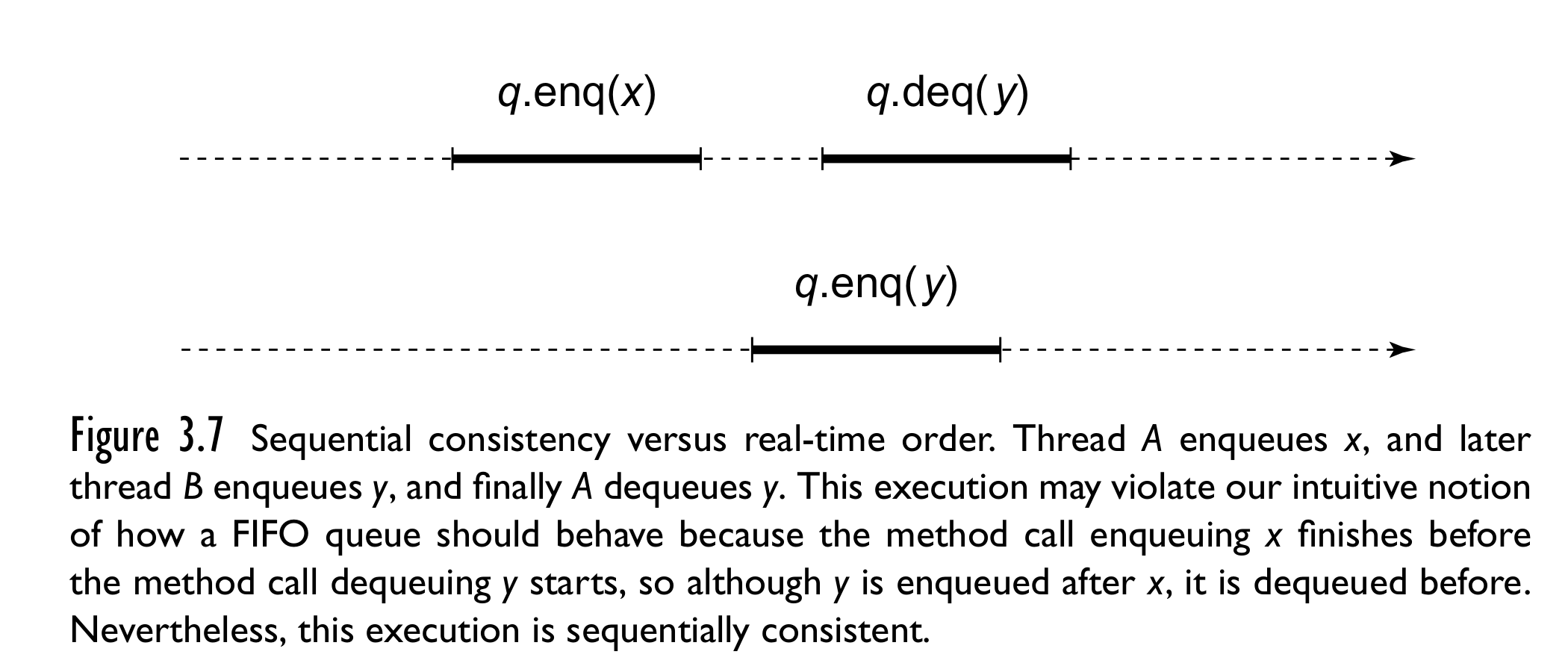
上面这个图也是满足SC的,虽然看起来违反直觉,但SC本身就是只关心program order,不关心现实中的先后顺序。且SC不具有compositional的性质,举例如下
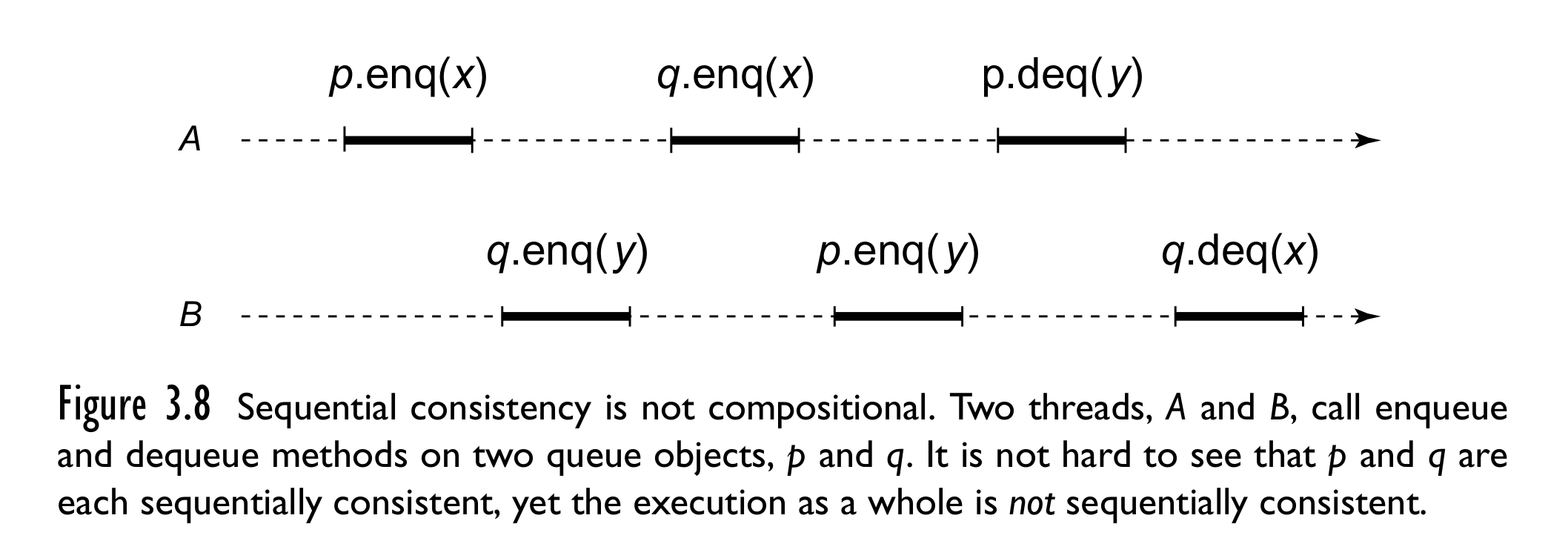
从P,Q分别满足SC可以推导出,上图中的事件存在环。
4. VERIFYING THAT IMPLEMENTATIONS ARE LINEARIZABLE
### 4.1 Definition of Correctness
An implementation is a set of histories in which events of two objects, a representation (or rep) object REP of type REP and an abstract object ABS of type ABS. 对于implementation中的每一个history \(H\),有(1). the subhistories \(H \vert REP\) and \(H \vert ABS\) satisfy the usual well-formedness conditions; (2). 对每个进程\(P\), each rep operation in \(H \vert REP\) lies within an abstract operation in \(H \vert P\)
An implementation is correct with respect to the specification of ABS if for every history \(H\) in the implementation, \(H \vert ABS\) is linearizable.
4.2 Representation Invariant and Abstraction Function
后续证明不好懂,等有需要时再更新,目前了解Linearizability概念即可。