The Byzantine Generals Problem
1. INTRODUCTION
想象拜占庭军队被分成几个部分,独立驻扎在敌军城市外围,每个分部由自己的将军(general)指挥。将军之间可以通过信使(messenger)互相沟通。在观察敌军情况后,他们必须决定一个共同的行动计划。然而,有些将军可能是叛徒,会阻止忠诚将军达成一致。
因此,将军们需要一个算法来保证
A. All loyal generals decide upon the same plan of action. 忠诚将军们不光要达成一致,还需要行动计划是reasonable的
B. A small number of traitors cannot cause the loyal generals to adopt a bad plan.
对每个将军来说,需要观察敌人情况和了解其他将军的意见。让$v(i)$代表收到的第$i$个将军的消息,那么每个将军就会基于$v(1)$,…,$v(n)$做决策。如果所有将军都使用同一套方法做决策,那么条件A就满足;要满足条件B需要使用robust method,比如投票选大多数的决定,叛徒只有在进攻和撤退票数差不多时才能发挥作用,而这时本身也难说进攻或撤退哪个是bad plan。
但这种办法其实有问题,因为条件A需要每个诚实将军收到相同的消息,而叛徒可以给不同的将军发送不同的消息。为了保证条件A,需要满足以下条件:
1 Every loyal general must obtain the same information $v(1)$,…,$v(n)$
这个条件表明将军不能直接使用收到的消息,因为自己收到的消息可能和别人不同。此外,再引入一种可能,将军收到的消息可能和实际发出的消息不同(即使发消息的是忠诚将军)。为了防止这种情况发生,再对每个将军要求如下:
2 If the $i$th general is loyal, then the value that he sends must be used by every loyal general as the value of $v(i)$.
也可以再重写条件1,对每个将军要求如下:
1’. Any two loyal generals use the same value of $v(i)$
条件1’和条件2都是关于单条消息的要求。然后考虑发送方的情况,提出下面的问题
Byzantine Generals Problem. A commanding general must send an order to his n-1lieutenant generals such that:
IC1. All loyal lieutenants obey the same order.
IC2. If the commanding general is loyal, then every loyal lieutenant obeys the order he sends.
IC1和IC2被称为the interactive consistency conditions。如果commander是忠诚的,那么可以从IC2推导出IC1.然而,commander不全是忠诚的。为了解决原始问题,第$i$个将军就需要通过拜占庭将军问题的解法,把自己的命令$v(i)$发出去。
2. IMPOSSIBILITY RESULTS
如果将军只能派人传达口头消息(oral message),那么必须保证超过2/3是忠诚将军,否则拜占庭将军问题无解。口信可以被信使任意篡改,这就类似计算机网络中的消息传递,在第4部分会使用签名后的笔信来防篡改。
然后阐述在只有3个将军的时候,即使只有一个叛徒问题也无解。在图一中,lieutenant1既收到attack,又收到retreat,他没有办法分辨哪个是忠诚的。而要满足IC2的话,他必须接受attack命令。(注: 所以,图一lieutenant1的优选看上去是一直遵守commander的命令,这样可以同时满足IC1和IC2)
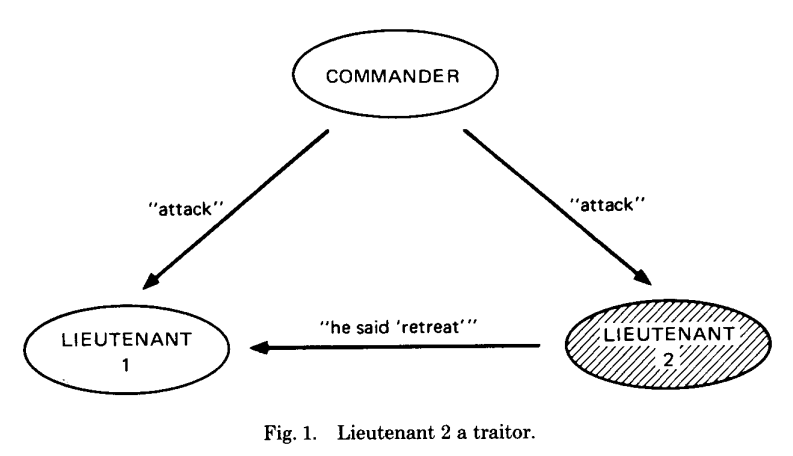
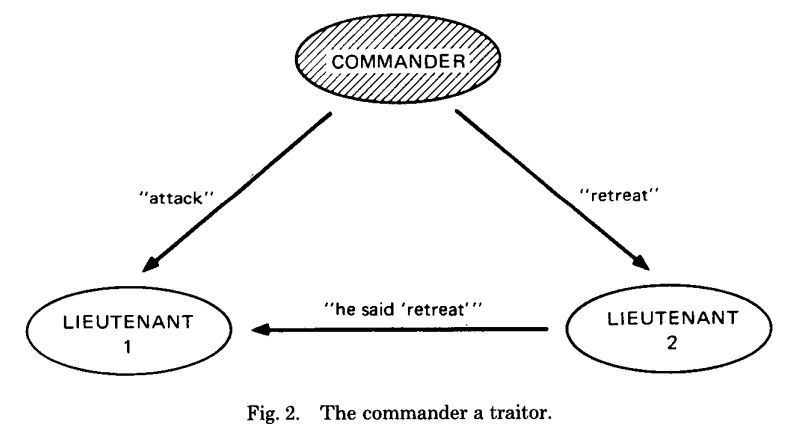
再看图二,如果commander是叛徒,lieutenant1实际上还是面临图一的情况,他无法分辨收到的消息哪个是真哪个是假。如果他选择遵守commander的指令选择attack,那么lieutenant可能会retreat,不满足IC1.(注: 图二lieutenant1的优选是不遵守commander,也可以同时满足IC1和IC2。但问题是,lieutenant1根本不知道自己是处于图一还是图二,所以问题无解)
有了上面的结果,我们可以证明如果有m个叛徒,将军总数小于3m+1的话就无解。证明方法是反证法,如果3m或更少的将军(为了区分,这里的将军被称为Albanian general)中有m个叛徒,这种情况下如果有解,那么可以构造出3个将军一个叛徒的解,与上文矛盾。three-general的解需要让每个拜占庭将军模拟三分之一左右的Albanian将军。因此,每个拜占庭将军最多模拟m个Albanian将军。拜占庭commander模拟Albanian commander和最多m - 1个Albanian lieutenant。由于我们假设了3m+1问题有解,It is easy to check that conditions IC1 and IC2 of the Albanian generals solution imply the corresponding conditions for the Byzantine generals, so we have constructed the required impossible solution.
(注: emmm…没觉得easy to check,不太清楚怎么推导的。假设Albanian commander是忠诚的,给每个将军都发送了attack命令,那么一个忠诚的lieutenant将会有2m - 1个将军(包括commander)告诉他要attack,另外m个叛徒告诉他要撤退,只要m > 1,那2m - 1 > m成立,感觉这里主要是不清晰将军间到底是怎么通讯的)
有人觉得解决拜占庭将军问题的难点在于到达成准确的一致(exact agreement),接下来阐述达成近似一致(approximate agreement)和准确一致是一样难的。假设将军只需要对进攻时间达成大概一致,而不是决定是否进攻或撤退。更准确地,需要commander指挥攻击时间,然后要求满足以下两个条件
IC1’ All loyal lieutenants attack within 10 minutes of one another.
IC2’ If the commanding general is loyal, then every loyal lieutenant attacks within 10 minutes of the time given in the commander’s order.
和拜占庭将军问题一样,这个问题中如果忠诚将军人数不超过三分之二的话也是无解。证明方法是,假设三个将军中一个叛徒的情况有解,那么也可以构造出拜占庭将军问题的解。假设commander发布进攻或撤退命令,在1:00进攻,2:00撤退。那么每个lieutenant将使用以下步骤来执行命令:
(1) 在收到commander的attack命令后,一个lieutenant做以下某一件事
(a) 如果时间是1:10或更早,则attack
(b) 如果时间是1:50或更晚,则retreat
(c) 如果都不是,去步骤(2)
(2) 询问其他某个lieutenant在步骤一中选择了哪一步
(a) 如果这个lieutenant在步骤(1)中有选择,就做同样的选择
(b) 否则,撤退.
如果commander是忠诚的,那么一个忠诚的lieutenant会在步骤(1)中获得正确的指令,因此IC2满足.如果commander是忠诚的,那么可以从IC2推导出IC1,所以我们只需要在假设commander是叛徒的前提下证明IC1. 从IC1’中可以推导出如果一个lieutenant在步骤(1)中决定进攻,那么另一个就不能在步骤(1)中决定撤退。因此,他们要么在步骤(1)产生同样的选择,要么至少一个跳转到步骤(2). In this case, it is easy to see that they both arrive at the same decision, so IC1 is satisfied.(注: easy to see? 这里的in this case是指要么在步骤(1)产生同样选择,要么至少一个到步骤(2)?是的话确实满足IC1 )。这样就构造了拜占庭将军问题的three-general solution,与已知矛盾。
3. A SOLUTUION WITH ORAL MESSAGES
接下来阐述3m+1或更多将军中m个叛徒的解。首先定义”oral messages”,每个将军需要执行相应的步骤来发送消息给其他将军。我们假设忠诚将军会按要求执行步骤。定义消息系统如下:
A1. Exery message that is sent is delivered correctly
A2. The receiver of a message knows who sent it
A3. The absence of a message can be detected.
条件A1和A2阻止了叛徒干扰两个将军的通信,A1可以防止消息内容被篡改,A2可以保证消息来源。如果叛徒决定故意不发送消息,那么A3也可以察觉到这一点。这个消息系统的实现在Section 6讨论。
在本节和下一节的算法中,要求每个将军能直接给其他所有将军发消息。在Section 5,描述的算法可以不要求这个保证。
一个叛徒commander可能决定不发出任何命令。由于副官们必须遵守一样的命令,在这种情况下他们需要默认的命令。我们让撤退成为默认命令。
我们定义一个Oral Message 算法OM(m),m为非负整数。我们将阐述OM(m)算法可以解决拜占庭将军问题在有3m+1或更多将军的情况下,能解决最多m个叛徒的问题。