阅读 Time, Clocks, and the Ordering of Events in a Distributed System

Introduction

​ 现实世界中，我们习惯有时间的概念，而且事件发生有先后顺序，before或者after。分布式系统由多个时空分隔的进程组成，以交换信息的方式通信。一台计算机也可以被看做是分布式系统，因为计算单元，存储单元，IO单元等由不同进程组成。如果消息传递延迟和单个进程中事件间隔时间比不可忽略时，系统就是分布式的。

​ 本文主要关注时空分隔的不同计算机组成的分布式系统。分布式系统中有时不可能知道两件事件哪一个先发生。”happened before”关系在系统中只是一种偏序(partial ordering)关系。本文将讨论由happened before原则定义的偏序关系，然后给出分布式算法将其拓展为所有事件的一致性全序(consistent total ordering)

注： 什么是偏序和全序？

​ 偏序和全序并不是论文中的内容，这里只是简单作为前置知识补充说明

如果集合中的某种关系满足以下3个性质，那么这个关系是偏序(Partial Order)

• Reflexivity: 集合中所有元素a，都有aRa
• Antisymmetry: 如果aRb且bRa，那么a=b(或者说a不是b的话，如果aRb，那么bRa不成立)
• Transitivity: 如果aRb且bRc，那么aRc

全序是偏序的一种特殊情况，全序可以对集合中任意两个元素进行比较，但偏序不能，偏序只能在部分元素间进行比较

The Partial Ordering

​ 如果a在比b之前的某个时刻先发生，大多数人会说事件a比事件b先发生(happened before)，但这种断言可能只有在物理学时间理论中成立。实际上，如果系统正确满足某种规范(specification)，那么这种规范必须给出系统中可观测事件的依据。如果规范以物理学中的时间理论为依据，那么系统就必须有物理时钟。但即使有了时钟，时钟本身也不是完全准确而导致会出现问题。因此我们不使用物理时钟而定义了”happened before”关系

​ 我们首先更准确地描述我们的系统。我们假设系统由一系列进程组成，每个进程包含一系列顺序事件。取决于应用程序自身，可以将一台计算机上运行的一段子程序看作一个事件，也可以将一条机器指令的执行看作一个事件。我们假设一个进程有事件序列，如果事件a比事件b先发生，那么事件a在序列中的位置比b靠前。换句话说，单个进程由一系列具有priori total ordering性质的事件组成

​ 我们假设在一个进程中发送或接收消息是一个事件。我们可以定义happened before关系，用→表示

​ 定义: 一个系统中的事件集合上的关系→满足以下3个条件

• 如果a和b是同一个进程中的事件，且a比b先发生，那么a→b
• 如果a是一个进程发消息，而b是在另一个进程接收这一条消息，那么a→b
• 如果a→b且b→c，那么a→c。如果a→b和b→a都不成立，那么两个不同的事件a和b是并发的(注: 这一条就说明→只能是偏序关系了，因为两个并发事件不能比较先后顺序)

​ 我们设定a→a不成立，因此在系统中→是irreflexive partial ordering(注: 这里就和普通的偏序略有差别了，普通偏序是有自反性的)

​ 接下来看下space-time diagram中关于上述定义的解释。

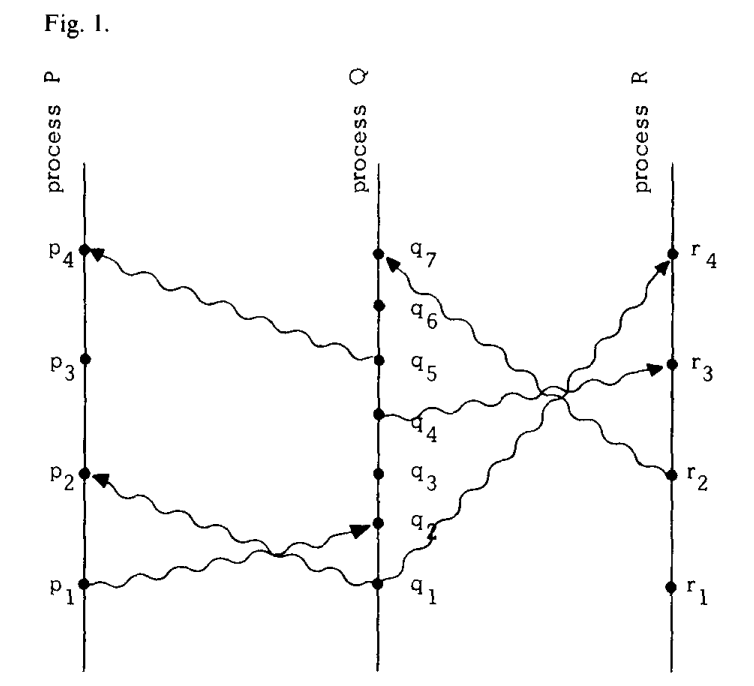
​ 水平方向代表空间，竖直方向代表时间，且时间向上增长，点代表事件，竖直线代表进程，波浪线代表消息。很容易发现a→b意味着可以从点a沿着进程线或消息线向上移动到b点。比如在图一中p1→r4

​ 另一种解读视角是a→b代表事件a可能影响到事件b。如果两个事件不能相互影响，那么它们是并发的。比如图一中事件p3和q3，虽然从图中能看出q3在物理世界中先发生，但进程P并不知道进程Q在q3的结果，直到p4接收了进程Q的消息。(在p4之前，P最多知道进程Q打算在q3做什么)

​

Logical Clocks

​ 现在为系统引入时钟，一开始的抽象时钟只是为事件分配一个编号。更准确的说，为每个进程\(P_i\) 定义一个时钟\(C_i\)，时钟将为进程中的每个事件\(a\)分配编号\(C_i\langle a\rangle\) 。目前认为这是一个逻辑时钟，可以通过计数器实现而不借助任何真正的计时工具。

​ 然后考虑这样的时钟系统正确性意味着什么，我们不能基于物理时间的定义，我们只能基于事件发生的先后顺序。最严格的条件是如果事件a发生在事件b之前，那么事件a应该在事件b发生前的某个时间发生，更正式的，有:

• Clock Condition: for any events a, b: if a → b，那么\(C\langle a\rangle\) < \(C\langle b\rangle\)

​ 注意我们不能从\(a\nrightarrow b\)推导出两者时钟上的关系。但可以从\(\rightarrow\) 关系中推导出其满足以下两个条件

• C1. if a and b are events in process \(P_i\), and a comes before b, then \(C_i\langle a\rangle < C_i\langle b\rangle\)
• C2. if a is the sending of a message by process \(P_i\) and b is the receipt of that message by process \(P_j\), then \(C_i\langle a\rangle < C_j\langle b\rangle\)

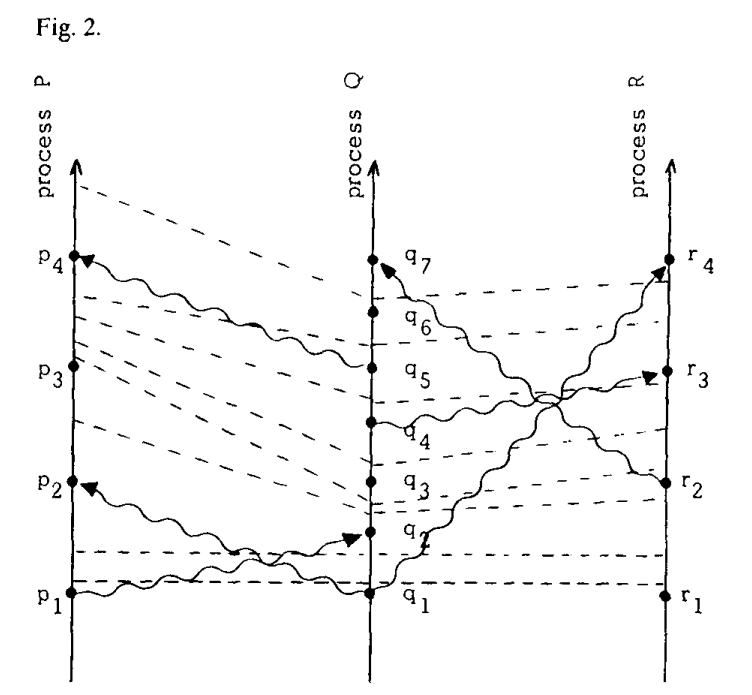
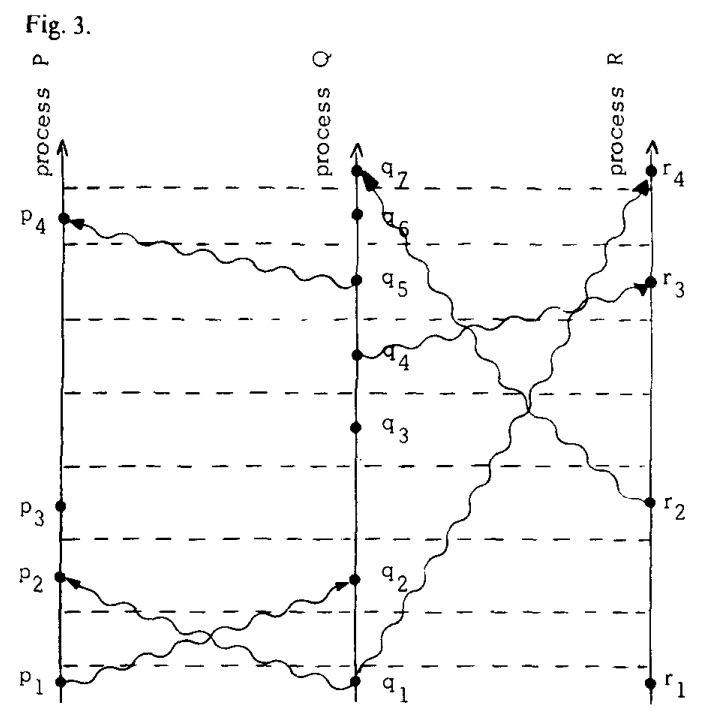
​ 重新考虑space-time图中的时钟，我们假设进程时钟会经过每一个数字，比如在某个进程中，事件a发生在数字4，事件b发生在数字7，那么二者间隔中，时钟经历了5、6、7。我们在图一的基础上绘制点状的tick line得到图二。条件C1意味着一个进程中任意两个事件间都有一条tick line，条件C2意味着每条消息线都必须穿过一条tick line。

​ 我们可以把tick line看作是某个笛卡尔坐标系的时间坐标轴，然后在图二的基础上拉直这些tick line。在没有引入物理时间概念(需要引入物理时钟)时，不能区分图二和图三哪种表达方式更好。

​ 让我们假设这些进程是算法，事件代表进程执行过程中的某个动作。接下来将展示如何引入时钟(仍然是逻辑时钟)到进程且满足时钟条件(Clock Condition)。进程\(P_i\)的时钟由一个寄存器\(C_i\)表示，\(C_i\)的值会在事件间改变，因此其值的改变并不代表有新的事件产生。

​ 为了保证系统满足Clock Condition，我们需要保证满足C1和C2。条件C1很简单，只用遵守以下实现规则:

• IR1. Each process \(P_i\) increments \(C_i\) between any two successive events

​ 为了满足条件C2，我们需要每条消息m包含一个时间戳\(T_m\)，\(T_m\)的值就是该消息发送出去的时间。当进程收到一个时间戳为\(T_m\)的消息时，其必须快进时钟到大于\(T_m\)的时刻，准确地说，有以下规则

• IR2. (a) If event a is the sending of a message m by process \(P_i\), then the message m contains a timestamp \(T_m = C_i\langle a\rangle\)

  ​ (b) Upon receiving a message m, process \(P_j\) sets \(C_j\) greater than or equal to its present value and greater than \(T_m\)

​ 在IR2(b)中，我们认为接收消息m的事件发生在设置\(C_j\)后。很明显，IR1和IR2保证满足了Clock Condition

Ordering the Events Totally

​ 我们可以使用满足Clock Condition的时钟系统来为所有的事件排序。我们可以简单根据事件发生的时间进行排序。为了打破平局的情况(注: 指事件时钟相同)，我们使用进程的任意全排序(total ordering)\(\prec\) (注: 可以先简单理解为给每个进程分配了互不相同的优先级)。更准确地，定义以下一种关系\(\Rightarrow\) :

​ 如果a是进程\(P_i\)的事件，b是进程\(P_j\)的事件，那么\(a\Rightarrow b\)有且只有当(1)\(C_i\langle a\rangle < C_j\langle b\rangle\) 或者(2) \(C_i\langle a\rangle = C_j\langle b\rangle\)且\(P_i \prec P_j\)

​ 很容易看出这定义了全序关系，且Clock Condition暗示了如果\(a \rightarrow b\) 则有\(a \Rightarrow b\)。也就是说，关系\(\Rightarrow\)是补充了happened before的偏序关系为全序关系

​ 关系\(\Rightarrow\)取决于系统的时钟\(C_i\) ，并且不唯一。满足Clock Condition的不同时钟选择会产生不同的关系\(\Rightarrow\).给定任何从关系\(\rightarrow\)扩展来的关系\(\Rightarrow\)，总有一种时钟系统能满足Clock Condition且生成关系\(\Rightarrow\)。只有关系\(\rightarrow\)是由系统的事件唯一确定的

​ 能对所有事件全排序对实现分布式系统是非常有帮助的。实际上，正确实现逻辑时钟的原因就是为了获得这样的全序关系。使用这种全序关系，可以解决以下问题。

​ 考虑有一个系统由几个固定进程组成，进程共享一个资源。资源一次只能被一个进程使用。我们希望找到一种算法，使以下三个条件成立

(1). 一个进程被授权使用资源后，在资源下一次被授权给另一个进程前，必须先释放资源

(2). 不同的资源请求必须按它们产生(发起请求的时间)的顺序依次满足(注: 和常见的FCFS不太一样，这里是生成请求的时间，不是请求到达某个coordinator的时间)

(3). 如果每个进程最终都释放了申请到的资源，那么每个请求最终都能被满足

​ 我们假设资源最开始被赋予了某一个进程。 这些条件是非常自然的，条件(2)说明了处理两个并发请求的顺序。

​ 需要认识到这不是一个小问题，使用中心化调度程序，按接收请求的顺序授权资源是错误的，除非有更多的场景假设。比如假设P0是中心调度程序，P1发送了资源请求消息给P0，然后P1又发消息给P2。可能P2先收到P1的消息，然后也发资源请求给P0，有可能P2的请求比P1请求先到达。如果P0按接收顺序给P2授权，就违反了上面的条件(2)。

​ 为了解决这个问题，实现一套满足IR1和IR2的时钟系统，并且使用它们定义所有事件的全序关系\(\Rightarrow\) .这样就为所有请求操作和释放操作确定了顺序，有了这种顺序，再去寻找正确的算法就很容易，只需要让每个进程知道其他进程的操作。

​ 为了简化这个问题，做一些假设，这些假设不是必须的，但可以让我们避免陷入太多细节。首先假设对所有的任意两个进程\(P_i\)和\(P_j\)，消息从\(P_i\)到\(P_j\)的接收顺序和发送顺序一样。而且我们假设每条消息最终都能到达(这种假设可以避免引入消息编号和消息确认协议)，另外假设每两个进程间可以直接通信。

​ 每个进程维护一个别人看不见的request queue。我们假设request queue最初包含单条消息\(T_0:P_0\) request resource，\(P_0\)是最开始被授权资源的进程，\(T_0\)小于任何时钟的初始值。

​ 算法按以下5条规则定义(rule)。为了方便，认为每条规则的动作都是单个事件

1. 为了请求资源，进程\(P_i\) 发送消息\(T_m:P_i\) request resource给其他所有进程，并且把这条消息放入自己的request queue。\(T_m\)是消息的时间戳

2. 当进程\(P_j\)接收到消息\(T_m:P_i\) request resource ，将这条消息放进自己的request queue并且发送一条带时间戳的确认消息给\(P_i\)

3. 为了释放资源，进程\(P_i\)从request queue中移除所有\(T_m:P_i\) request resource消息并且发送一条带时间戳的\(P_i\) release resource消息给其他所有进程

4. 当进程\(P_j\)收到\(P_i\)的release消息，就移除其request queue中所有的\(T_m:P_i\) request消息

5. 进程\(P_i\)被授权资源时需要满足两个条件

   (a) 有一条\(T_m:P_i\) request消息在其request queue中且比队列中其他所有请求按关系\(\Rightarrow\)(消息按发送时间排序)都更早

   (b) \(P_i\)在\(T_m\)时间后有收到其他所有进程的消息(注: 没有规定一定是ACK)

​ 需要注意条件5是完全由\(P_i\)自己在本地检测的。

​ 容易证明上述算法满足上文的条件(1)~(3)。首先，观察rule5的条件(b)，同时有消息按顺序接收的假设，保证了\(P_i\)已经知道了在自己请求前的所有请求。由于只有rule3和4可以删除request queue中的消息，可以证明条件(1)成立。

(注: 证明: 如果条件(1)不成立，即资源在被下次授权前没有释放的话，那么request queue中就还有本次已获得授权的请求，破坏了rule5中条件(a) )

​ 条件(2)成立的原因是定义了全序关系，而且rule2保证了在\(P_i\)发起请求后，rule5 (b)最终会成立。

(注: 这里不是很懂为什么这样证明了条件2成立？一种粗浅的理解: 我猜这个request queue存消息应该是按全序关系排序的？那么这样的话两个几乎同时发起的请求之间有确定的先后顺序。假设现在两个进程一前一后非常近时间地发起了请求，进程A的请求先于进程B的请求，在A和B收到对方的请求之前(消息延迟)，各自请求在自己的request queue中都是排名第一的，这时如果没有rule5 (b)，A和B会同时获取资源。而造成这个问题的原因是A和B各自发起的请求都还没有完全通知到其他进程，因此rule5 (b)实际确保了进程发起的请求已经通知到其他所有进程。这里还有一点比较tricky的是，这个问题首先就假设好了消息从进程\(P_i\)到进程\(P_j\)的接收顺序和发送顺序一样，即消息是FIFO的，那么进程A在收到自己的确认前一定收到了B的请求，进程B在收到自己的确认前也一定收到了A的请求。再进一步，进程A在收到某个确认X时，一定收到了进程X发出确认前的所有请求(我们并不关心发出确认后的请求，因为之后的请求一定比A当前的请求晚)。所以进程A收到所有确认时，实际是和所有其他进程沟通好了当前请求和其他请求的相对位置)

​ Rule3和4意味着如果每个被授权资源的进程最终都能释放资源，那么rule5 (a)最终会成立，这证明了条件3.

​ 这是分布式算法，每个进程独立遵守运行规则，不依赖中心调度或中心存储。可以把这种同步机制特定为状态机(State Machine)，状态机的command是request resource或release resource，state是a queue of waiting request commands，队列头是当前被授权的请求，有新的请求发来时，添加到队列尾。

​ 每个进程可以独立模拟状态机的执行过程。因为所有commands可以按全序关系排序，因此每个进程会看见相同的命令顺序。一个进程可以执行时间戳为T的命令，当且仅当已经了解到其他所有时间戳小于等于T的命令。这种方法可以在分布式系统中实现任意需要的多进程同步，但却需要所有进程都是active的，如果某一个进程挂了，则整个系统崩溃(注: 不满足rule 5(b)了)。

Anomalous Behavior

​ 这套调度算法利用全序关系为请求排序，这允许了以下一种anomalous behavior: 假设有一套国家范围内计算机组成的系统，一个人在计算机A上发起了请求，然后他打电话给在另一个城市的朋友，让朋友在另一台计算机B发出请求B。那么很有可能请求B携带更小的时间戳，并且排序在请求A之前。这种情况发生的原因是系统没有办法知道A实际比B更先，因为关于顺序的信息是存在于系统之外的。

​ 有两种办法解决这个问题，一是把需要的信息也纳入系统中，比如上文中的请求A从系统中获取时间戳A，请求B从系统中获取时间戳B，那么系统会保证时间戳B一定晚于时间戳A。另一种办法是构造更强的时钟条件:

• Strong Clock Condition: 如果系统事件a比b先发生(包含外界信息的情况) \(a \mapsto b\)，则C(a) < C(b)

可以通过引入物理时钟构造Strong Clock Condition。

注: 这里\(a \mapsto b\) 的含义是，事件a 和 b 之间有某种系统感知外的前后关系，但无论是哪种具体的前后关系，在现实世界，总是需要某种消息从a发出，经过一段实际的时间间隔(物理时间，因此需要引入物理时钟)才到达b，这时需要保证b分配的时间要大于a

Physical Clocks

引入物理时钟到系统中，设在物理时间\(t\) 读时钟 \(C_i\) 的值为 \(C_i(t)\)，为了方便，我们设定时钟是连续的而不是离散的。更正式的，假设\(C_i(t)\) 是连续，可微的函数，只有在时钟被重置时发生跳跃。考虑到物理时钟的实际情况，需要保证 \(dC_i(t) / dt \approx 1\) for all t. 更正式的，需要保证下面的条件

• PC1 There exists a constant \(\kappa \ll 1\) such that for all \(i: \left\vert dC_i(t) / dt - 1 \right\vert < \kappa\)

此外，还要保证各个进程的时钟误差不大

• PC2 For all \(i, j\) : \(\left\vert C_i(t) - C_j(t) \right\vert < \epsilon\)

由于不同时钟一定不会按相同速率运行，误差会越来越大，因此需要某种机制进行时钟同步，来保证PC2永远成立。

但是首先，需要确定\(\kappa\) 和 \(\epsilon\) 要多小才能避免anomalous behavior. 假设我们的时钟满足普通的Clock Condition，则只需要考虑不同进程事件\(a \nrightarrow b\)的情况

引入一个变量 \(\mu\)，设事件 \(a\) 发生在物理时间 \(t\) , 另一个进程的事件 \(b\) 满足 \(a \mapsto b\) ，则 \(b\) 发生在\(t + \mu\) 之后。显然，\(\mu\) 需要比所有进程间通讯延迟更短，可以让 \(\mu\) 等于距离除以光速，但实际上可以更大。

为了避免anomalous behavior，需要保证对任意的 \(i, j, t\) 有 \(C_i(t + \mu) - Cj(t) > 0\) ，从PC1可以推导出\(C_i(t + \mu) - C_i(t) > (1 - \kappa)\mu\) ，再结合PC2，可以证明当 \(\epsilon /(1 - \kappa) \le \mu\) 时， \(C_i(t + \mu) - Cj(t) > 0\) 成立，即此时不会有anomalous behavior。另外，在调节时钟时，只能往后调，否则可能违反C1。

接下来描述让PC2成立的一种实现。让\(m\) 是在物理时钟 \(t\) 时刻发送，\(t'\) 接收的消息。定义\(v_m = t' - t\) 为总延时(total delay). 这个延时对接收进程来说是不可知的，但我们可以引入一个 minimum delay \(\mu_m \ge 0\) 且 \(\mu_m \le v_m\)，我们称\(\xi_m = v_m - \mu_m\) 为unpredictable delay. 然后给出实现的两个要求

• IR1’ for each \(i\), if \(P_i\) does not receive a message at physical time \(t\), then \(C_i\) is differentiable at \(t\) and \(dC_i(t) / dt > 0\) (注: 就是时钟必须严格递增)
• IR2’ (a) If \(P_i\) sends a message \(m\) at physical time \(t\), then \(m\) contains a timestamp \(T_m = C_i(t)\) (b) Upon receiving a message \(m\) at time \(t'\) , process \(P_j\) sets \(C_j(t') = max(C_j(t' - 0), T_m + \mu_m)\) (注意不是\(v_m\))

为了简便，只考虑事件发生在某个准确的物理时刻，且同一进程的不同事件发生的时刻不同。不需要考虑实际上事件会持续一小段时间，而要关心离散时钟频率是否够快，如果慢了就不能保证C1。

个人总结： 文章首先指出分布式系统中的事件关系为偏序关系，基于此我们可以再得到某种全序关系对所有事件排序，然后可以得到一种同步互斥的算法。另外由于系统看到的只有它本身，只能通过有限信息和外界交流，但它们又都实际存在于同一个现实世界，且我们人类是在现实世界进行观察，因此需要引入物理时钟作为同一个参考系。本文证明了只要时钟足够精确，就可以避免出现异常行为。